Ch. 15 Hardware

15.1 Processors and parallel processing

RISC and CISC processors

RISC: Reduced instruction set computer

CISC: Complex instruction set computer

RISC processors

Breaking up the assembly code instructions into a number of simpler single-cycle instructions

Optimised set of instructions

Fewer built-in instruction formats

Higher processor performance

CISC processors

Based on single complex instructions which need to be converted by the processor into a number of sub-instructions to carry out the required operation

Makes use of more internal instruction formats

Carrying out a given task with minimal lines of assembly code

Hardware must be capable of handling more complex assembly code instructions

RISC	CISC
Fewer instructions	More instructions
Simpler instructions	More complex instructions
Smaller number of instruction formats	Many instruction formats
Single-cycle instructions whenever possible	Multi-cycle instructions
Fixed-length instructions	Variable-length instructions
Only load and and store instructions to address memory	Many types of instructions to address memory
Fewer addressing modes	More addressing modes
Multiple register sets	Fewer registers
Hard-wired control unit	Microprogrammed control unit
Pipelining easier	Pipelining more difficult

Pipelining

Perk of RISC

Allows several instructions to be processed simultaneously without having to wait for previous instructions to be completed

Interrupts

Once the processor detects the existence of an interrupt, the current program would be temporarily stopped and the status of each register is stored

The processor can be restored to its original status

Parallel processing

SISD (Single instruction single data stream)

Uses a single processor

Handles a single instruction which uses one data source at a time

Each task is processed in sequential order

Does not allow for parallel processing

Found in early personal computers

SIMD (Single instruction multiple data stream)

Uses many processors

Each processor executes the same instruction but uses different data inputs

Doing the same calculations but on different data at the same time

“Array processors”

Application in graphic cards
- For example, the brightness of an image made up of 4000 pixels needs to be increased
- Can work on many data items at the same time, so 4000 small processors can each alter the brightness of each pixel by the same amount at the same time

Application in sound sampling, or any application where a large number of items need to be altered by the same amount

MISD (Multiple instruction single data stream)

Uses many processors

Each processor uses different instructions but uses the same shared data source

Implemented in a fault-tolerant system

Output would only be accepted if the same output was produced by all the processors

MIMD (Multiple instruction single data stream)

Similar to SIMD with more than one processing unit receiving the parallel data streams

The difference is that each processing unit does not execute the same instruction

Multiple data stream can be provided by a single memory

Parallel computer systems

The MIMD architecture can be implemented in multicomputer systems known as massively parallel computers

Used by large organisations for computations involving highly complex mathematical processing

By linking computers together in this way

Massively increases the processing power of the single machine

Each processor will carry out part of the processing

Communication between computers is achieved via interconnected data pathways

15.2 Boolean algebra and logic circuits

Boolean algebra

Commutative Laws	A + B = B + A	A.B = B.A
Associative Laws	A + (B + C) = (A + B) + C	A.(B.C) = (A.B).C
Distributive Laws	A.(B + C) = (A.B) + (A.C) (A + B).(A + C) = A + B.C	A + (B.C) = (A + B).(A + C)
Idempotent Laws	A.A = A	A + A = A
Identity Laws	1.A = A	0 + A = A
Null Laws	0.A = 0	1 + A = 1
Inverse Laws	A.!A = 0	A + !A = 1
Absorption Laws	A.(A + B) = A A + (A.B) = A	A + (A.B) = A A + (!A.B) = A + B
De Morgan’s Laws	!(A.B) = !A + !B	!(A + B) = !A.!B

Further logic circuits

Combination circuit (output depends entirely on the input values)

Two important logic circuits used in computers are

the half adder circuit

the full adder circuit

Half adder

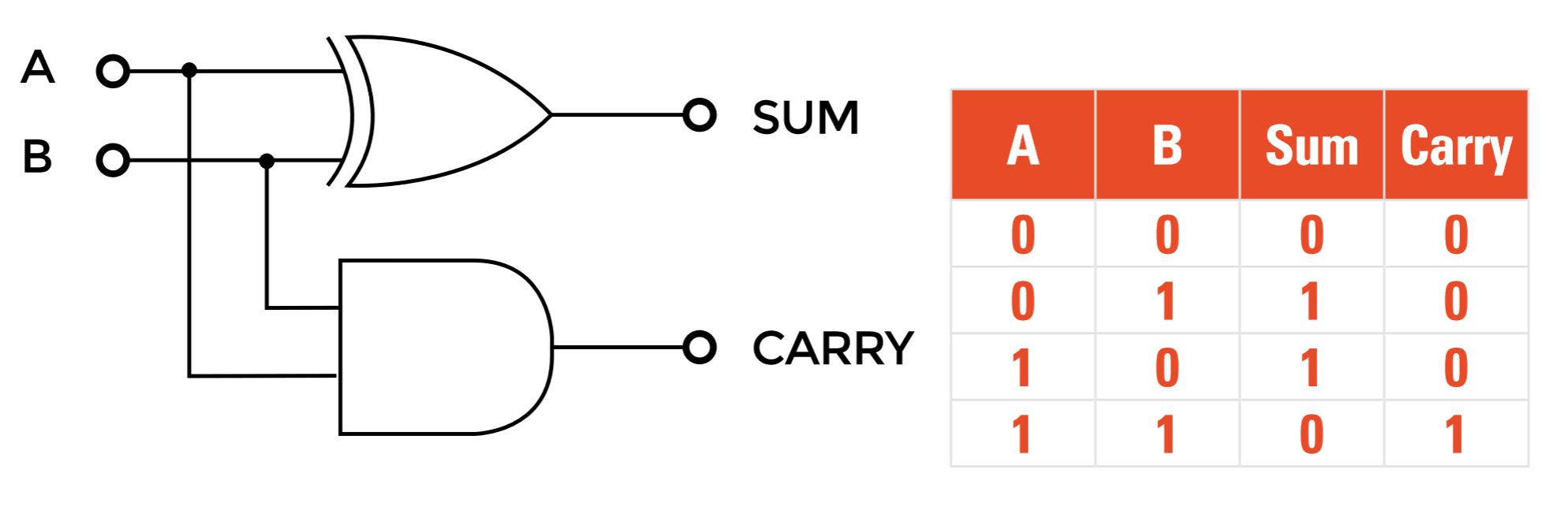
Simplest circuit

Carries binary addition on 2 bits generating two outputs
- the sum bit (S)
- the carry bit (C)

Cannot deal with the addition of several binary bits

Full adder

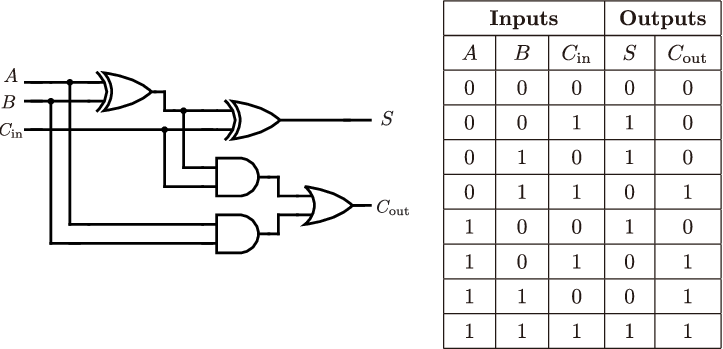
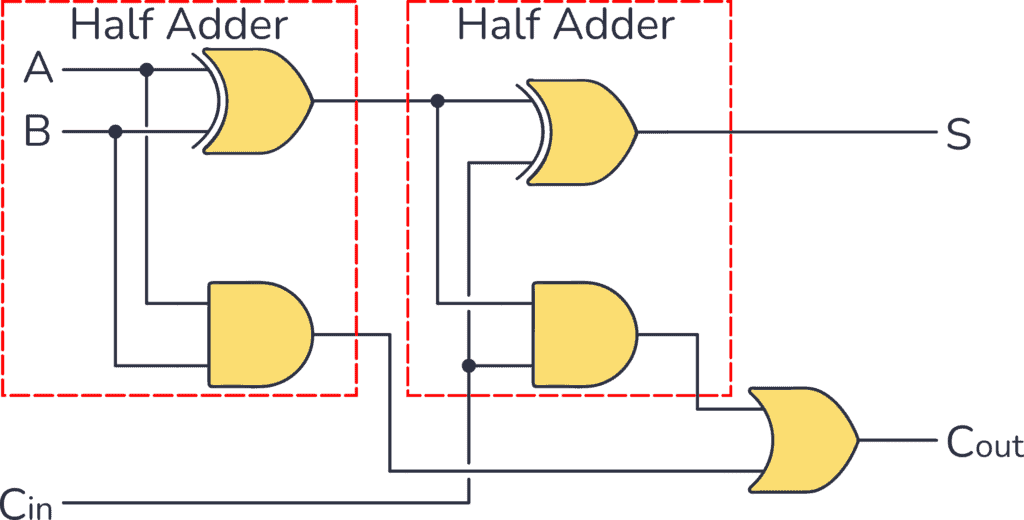
Formed of two half adders

To deal with the carry bit

Flip-flop circuits

Sequential circuit (output depends on the input value produced from a previous output value)

SR flip-flops

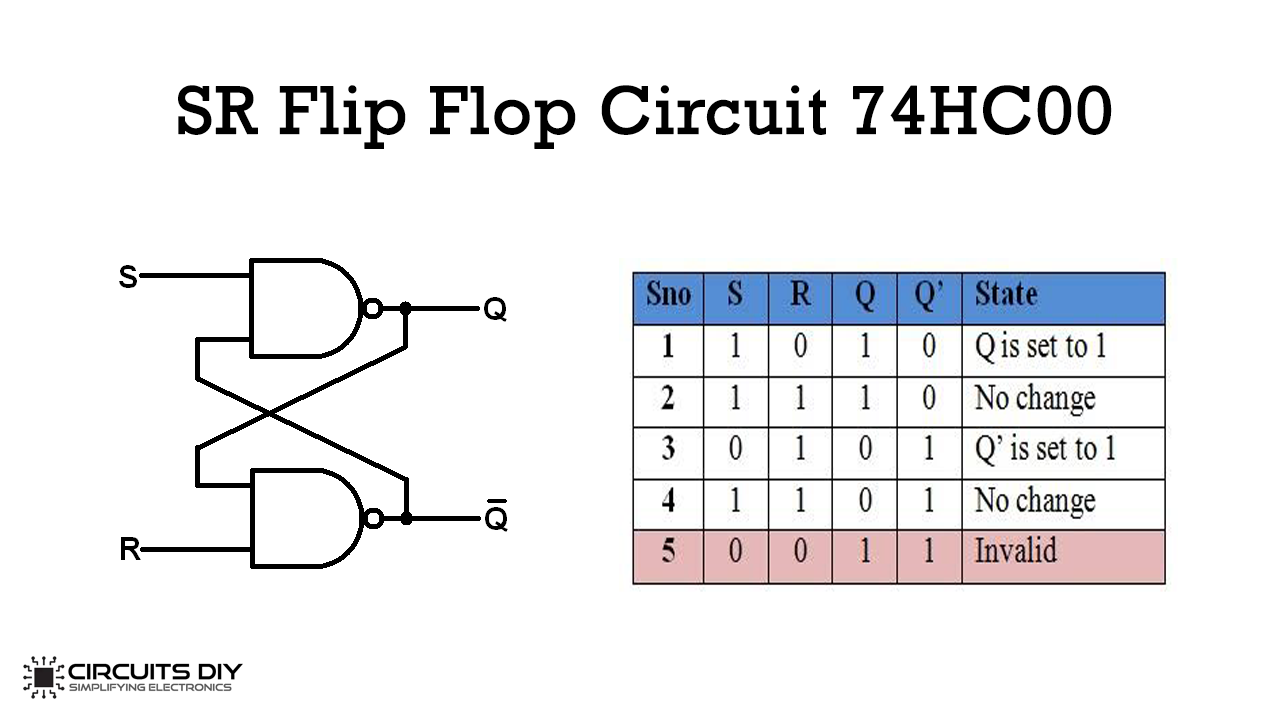
Consists of two cross-coupled NAND gates

Can be used as a storage/memory device for one bit

A value can be remembered but can also be changed

JK flip-flops

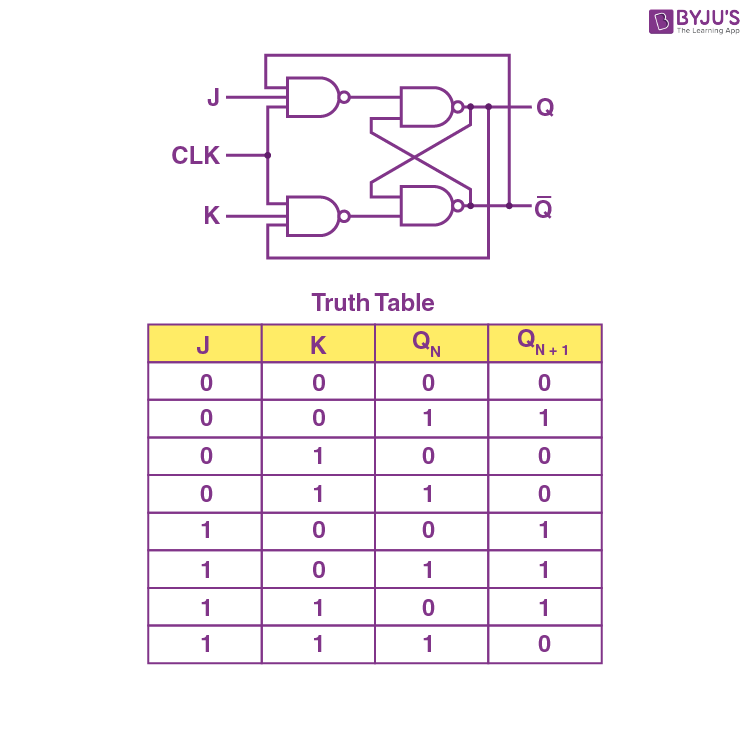
SR flip-flop problems
- Invalid S, R conditions need to be avoided
- If the inputs do not arrive in time, the flip-flop can become unstable

Several JK flip-flops can be used to produce shift registers in a computer

A simple binary counter can be made by linking up several JK flip-flop circuits

Boolean algebra and logic circuits

Karnaugh maps (K-maps)

The values along the top and the bottom follow Gray code rules

Only cells containing a 1 are taken account of

Groups can be a row, a column or a rectangle

Groups must contain 1, 2, 4, 8, or in general 2^n cells

Groups should be as large as possible

Groups may overlap within the above rules

Single values can be regarded as a group even if they cannot be combined with other values to form a larger group

The final Boolean expression can only consider those values which remain constant within the group (that is, remain a 1 or 0 throughout the group)